一、国际制单位 System de International
The SI – BIPM has set up the standard for measuring the quantity. Seven base unit is defined using the seven universal constants.
二、基本单位Base unit
这7个基本物理量 base quantity以及它们的对应单位分别是
| name | symbol | unit, full name | defining constant |
| time | t | s, second | unperturbed ground state hyperfine transition frequency of the caesium-133 atom ΔνCs is 9 192 631 770 Hz |
| length | l, s, d | m, metre | speed of light in vacuum c is 299 792 458 m/s |
| mass | m, M | ||
| thermodynamic temperature | T, $theta$ | K, kelvin | the Boltzmann constant k is 1.380 649 x 10–23 J/K |
| electric current | I, i | A, ampere | the elementary charge e is 1.602 176 634 x 10–19 C |
| amount of substance | n | mol, mole | the Avogadro constant NA is 6.022 140 76 x 1023 mol–1 |
| luminosity | Iv | cd, candela | the luminous efficacy of monochromatic radiation of frequency 540 x 1012 Hz, Kcd, is 683 lm/W |
The numerical values of the seven defining constants have no uncertainty.
The definitions of the base units specify the exact numerical value of each constant when its value is expressed in the corresponding SI unit.
All units of the SI can be written either through a defining constant itself, or through products or quotients of the defining constants.
三、前缀prefixes
The amount for 1 standard unit is sometimes not proper for certain physical quantities. For example, to measure the distance between two cities, using metre might be too burdensome for the geologists. To measure the length of a paramecium1, expressed in metre is too tiny for a biologist. Hence, using prefixes can create large or smaller unit.

Since in the numerical system, decimal2 system are used. The prefixes will enlarge or diminish the unit to a power of ten.
The table that list all the prefixes are listed below:
| Name | Symbol | Multiplying factor | Example |
| tera | T | 1012 | The SSD has 1TB3 of storage |
| giga | G | 109 | the frequency of wifi is 2.4GHz |
| mega | M | 106 | |
| kilo | k | 103 | The hair drier has a power of 1kW, which is against the regulation of BSWFL. Sorry |
| hecto | h | 102 | The atomspheric pressure is 101hPa |
| deca | da | 101 | |
| deci | d | 10-1 | the side length of a cube is 1dm |
| centi | c | 10-2 | an ant is nearly 2 cm long |
| mili | m | 10-3 | An adult can take in only 5mg of penicillin per time |
| micro | \[\mu\] | 10-6 | an bacterium usually measures 100 \[\mu\]m |
| nano | n | 10-9 | the wavelength for the visible light is 400-700 nm |
| pico | p | 10-12 | a laser surgery will exert 1ps of laser on human’s eyes |
There are also much larger prefix such as zetta, yotta, ronna, as well as the femto, atto, zepto. In Alevel, those are not required to master.
四、公制单位中的衍生单位Derived Unit in metric system
There would not be no question that the seven base unit is not enough for all the phenomena. For example, the voltage can not be measured in ampere, because the only base unit in electricity is ampere. Thus, there are a lot of derived units. The ability to derive the SI base unit of the derived unit is included in the learing objectives of A-Level.
The main principle is to derive the base unit from the defining formula
1. velocity/speed
There is no single name for the unit of velocity/speed. the SI base unit is m/s, it is derived as below:
\[v = \frac{\Delta s}{\Delta t}\]
\[[v] = \frac{[\Delta s]}{[\Delta t]} = \frac{\text{m}}{\text{s}}\]

2. acceleration
Still there is no common unit for the acceleration.
\[a = \frac{\Delta v}{\Delta t}\]
\[[a]=\frac{[\Delta v]}{[\Delta t]} = \frac{\text{m}/s}{\text{s}} = \text{m}\cdot \text{s}^{-2}\]
3. force
The common unit for the force is newton, N. The SI base unit for it is kg m s-2
The derivation is based on the Newton’s Second Law:
\[ F= ma\]
\[[F]= [m]\cdot [a] = \text{kg}\cdot \text{m}\text{s}^{-2}\]
\[1N = 1 \text{kg} \text{m}\text{s}^{-2}\]

4. moment & torque
Moment is the turning effect of forces, there is no common unit for moment, but we usually use Nm. The SI base unit for moment is kg m2 s-2
This can be done by using the definition of moment.
\[\text{moment} = \vec{F}\times \vec{r}\]
\[[\tau] = [F]\cdot [r] =\text{kg} \text{m}\text{s}^{-2} \times \text{m} = \text{kg} \text{m}^2\text{s}^{-2}\]
Pay attention to the unit of work/energy. You might find the two shares the same base unit. However, these two(three) physical quantities are not related since the difining formula is a cross product of two vectors.

5. Impulse
Impulse as the sum of accumulation of force with time, the unit for it is really simple to construct, it is Ns. The SI base unit for moment is kg m s-1
Because we define the impulse as the product of force and time.
\[\vec{I} = \vec{F}\cdot \Delta t\]
\[[I] = [F]\cdot [\Delta t] =\text{kg} \text{m}\text{s}^{-2} \times \text{s} = \text{kg} \text{m}\text{s}^{-1}\]
Pay attention to momentum, you might find it is exactly the same base unit with the momentum. This time for this pair, they are closely related to each other.

6. momentum
Momentum, as the product of the mass and velocity of an object, has the unit of kg m s-1 . The derivation process is quite simple.
\[\vec{p} =m \cdot \vec{v}\]
\[[p]= [m][v] = \text{kg} \times \text{m}\text{s}^{-1}\]
Pay attention to the equivalance of the impulse and momentum.
\[\vec{I} = \Delta {\vec{p}}\]
That is based on the homogeneity of the equation.

7. work
For this unit of work is used to memorize the great contribution of Joule, so the common unit is joule4. The base unit for joule is kg m2 s-2
Based on the definition of work done by a force.
\[ W = \vec{F}\cdot \vec{d}\]
\[[W] = [F] \cdot [d] = \text{kg} \text{m}\text{s}^{-2} \cdot \text{m} = \text{kg} \text{m}^{2}\text{s}^{-2}\]
Again, despite the joule shares the same base unit with the moment. The two physical quantities are not the same, you can compare them in the following ways:
- the scalar and vector nature of the two quantity
- the difference of the length and the displacement
- the cross and dot product of two vectors
So, there are no connection between work(energy) and moment.
8. energy
Energy is expressed in joules just like the work done. The base unit for joule is kg m2 s-2
And several formulae can be used to derive that.
\[ \text{k.e.} = \frac{1}{2} m v^2\]
\[ [k.e.] = [m][v]^2 = \text{kg} \cdot \left(\text{m} \text{s}^{-1}\right)^2 = \text{kg} \text{m}^2\text{s}^{-2}\]
You might try to use the defining formula of g.p.e. or e.p.e. to prove that again.

9. power
Power is usually measured in watt, in memorial of James Watt‘s great contribution in improving the steam engine. And the SI base unit for watt is kg m2 s-3

Again, definition of power is the rate at which work is done/energy is transferred.
\[ P = \frac{W}{\Delta t}\]
So, the derivation of watt in SI base unit is:
\[[P] = \frac{[W]}{[t]} =\frac{ \text{kg} \text{m}^2\text{s}^{-2}}{\text{s}} = \text{kg} \text{m}^2\text{s}^{-3}\]
Besides, due to the differential calculus. another formula to calculate the instanteous power is
\[P=\frac{\mathrm{d}\ W }{\mathrm{d}\ t} = \frac{\mathrm{d}\ Fs}{\mathrm{d}\ t} = F\cdot \frac{\mathrm{d}\ s}{\mathrm{d}\ t} = F\cdot v\]
You can also prove the SI base from newton and metre per second.
10. efficiency
There is no unit for the physical quantity- efficiency, since it is the ratio between the useful energy output and total energy input
\[\eta = \frac{\text{useful energy output}}{\text{total energy input}}\times 100\%\]
Since this quantity is dimensionless.
This would always remind me of the radian system, which express the angles with smaller value.
\[\pi \text{ or } 3.141592632\left(\text{in radian system}\right) = 180^\circ\left(\text{in degree system}\right)\] because the angle in radian is the ratio of the arc length to the length of the radius in the sectors.
11. density

As the first physical quantity, the unit of density of objects comes from the definition. The unit is kg m-3
the mass per unit volume
Hence,
\[\rho = \frac{m}{V}\]
\[[\rho]= \frac{[m]}{[V]} = \frac{\text{kg}}{\text{m}^3} = \text{kg}\text{m}^{-3}\]
Despite the common unit is expressed in kg and cubic metre, some times we prefer to use smaller units like g cm-3
e.g. Convert the density of gold 1.932*104 kg m-3 into g cm-3
\[1.932\times 10^4 \frac{\text{kg}}{\text{m}^3} \times \frac{\qquad\text{g}}{\qquad\text{kg}} \times \frac{\qquad \text{m}^3}{\qquad\text{cm}^3}\]
Try to fill in the values on the equation above.
12. pressure

The pressure is expressed in pascal, hence, it is used to honorize the French mathematican and physicist Blaise Pascal. We define the pressure as the
Force per unit area
So, let’s derive the SI base unit for pascal.
\[p = \frac{F}{A}\]
\[[p]= \frac{[F]}{[A]} = \frac{\text{kg} \text{m}\text{s}^{-2}}{\text{m}^2} = \text{kg} \text{m}^{-1}\text{s}^{-2}\]
Another way to formulate is the liquid pressure, which is calculated as
\[ p = \rho g h\]
You can use this to deduce that 1 Pa = 1 kg m-1 s-2
13. stress
Stress shares the same unit with presssure. But this quantity is occupied when we talk about the pressure inside an object like the stress in a string or a pilliar.
\[ \sigma = \frac{F}{A}\]
14. strain
Strain has no unit, because it is defined as:
the ratio of the extension to the orginal length (of a string)
\[\varepsilon = \frac{\Delta x}{\ell}\]
15. Young modulus

Since we use the ratio of stress to strain for a material. The unit is aligned with the stress. You might see that expression, an iron has a Young Modulus of 210GPa, while that of a carbon nanotube is 1000 GPa. Hence, the SI base unit is the same as pascal, which is kg m-1 s-2.
\[E = \frac{\sigma}{\varepsilon}\]
16. charge

Charge, as a physical quantity to describe the amount of electricity that an object carries, has the unit of coloumb. Obviously, the unit is named after the Charles-Augustin de Coulomb. The SI base unit for 1C is 1 As, comes from the formula
\[Q= I \cdot \Delta t \qquad \text{or}\qquad Q= \int I \mathrm{d} \ t \]
17. potential, voltage
Potential (Difference), or voltage has something to do with the charged particles in an electric field or in the circuit. The volt is used as the unit for both concept. Because it is the Alessandro Volta who first invented the battery sets. An interesting story is that Volta has shown his battery to the Napolean.

Electrical Potential is defined as:
work done per unit positive charge in moving it from infinity to a certain postion in the electric field.
Hence, the fomula to calculate the electric potential is
\[ V = \frac{W}{Q}\]
The unit of 1 V = 1 kg m-2 s-3A-1.
\[ [V] = \frac{[W]}{[Q]} = \frac{\text{kg} \text{m}^{2}\text{s}^{-2}}{\text{A}\text{s}} = \text{kg} \text{m}^{2}\text{s}^{-3}\text{A}^{-1}\]
Attention here, the volume and voltage and the unit of volt are expressed in V, but you shall decide based on the conditions.
From here, you might find it quite long and tedious to express the unit in SI base units. So, in electromagnetism, we prefer to use the common derive units instead of the SI base unit.
18. resistance
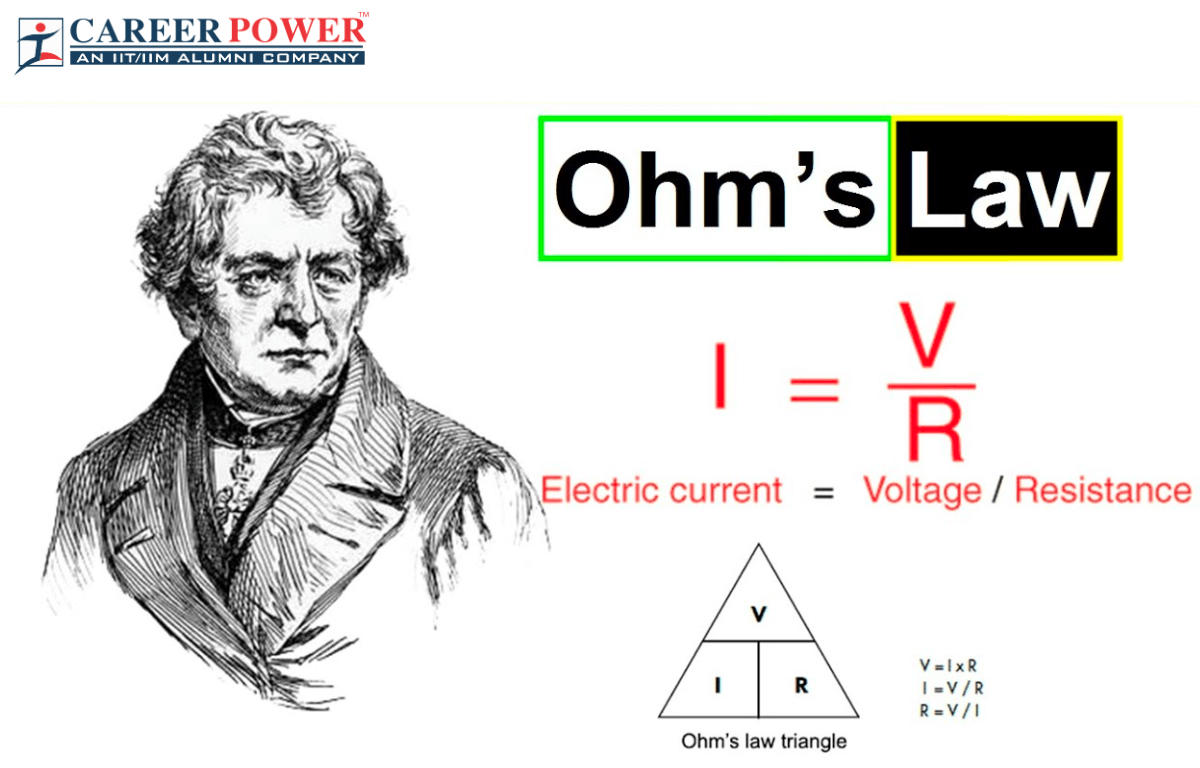
Thanks to the famous Ohm‘s Law, the unit of resistance in a resistor can be determined. The symbol is Ω. Pronouced as “Ohm”. But you shall know that this symbol comes from the greek letter, and pronouced as capitalized “omega”.
The SI base unit for ohm is kg m-2 s-3A-2
\[ R = \frac{V}{I}\]
\[[R] = \frac{[V]}{[I]} = \frac{\text{kg} \text{m}^{2}\text{s}^{-3}\text{A}^{-1}}{\text{A}} = \text{kg} \text{m}^{2}\text{s}^{-3}\text{A}^{-2}\]
Apart from resistor, we have capacitor, inductor, all of which are crictial electric components and have their own unique units.
19. frequency

You might find that we define the time, second from the frequency of the transition of caesium-133 atom. That is because frequency is the number times per second. The common unit in describing frequency is hertz. And Heinrich Hertz has made his own contribution to the radio waves phenonmena.
\[f = \frac{1}{T}\]
\[[f] = [T]^{-1} = \text{s}^{-1}\]
Therefore, 1 Hz = 1 s-1
20. wavelength
It is a length, so the unit for wavelength is m. There are no more induction in this unit.
However, when we investigate on the wavelength of the EM waves, nanometre is more preferred because they are usually very small. Using the prefix of nano (n) can make the digit normal.
You must memorize that
\[1 \text{nm} = 1\times 10^{-9} \text{m} = 0.000 000 001\text{m}\]
21. relative atomic mass unit
This unit is used to describe the mass of tiny particles such as the mass of nucleus, atoms, and molecules.
We introduce the unit of amu, and the definition of 1 amu is
1/12 of the carbon-12 atom
Hence, the base unit for amu is still kg, since it is still mass.
\[1\text{amu} = 1.66\times 10^{-27} \text{kg} \]