Question 1
1. Evidence of repeated reading:
单个题目数据的测量值需要至少测量两次,比如记录长度L,可以在空白的地方记录多次,最终数据值取平均值。marking scheme里面明确如下:
Evidence of repeat readings of V.
s18 qp34 Q1(b)
这里的一分不要忽略
2. Range of data SETS:
记录六组数据,要充分运用最大上限和最小下限。几乎每一套marking scheme里面对range of data都有明确规定。所以最大上限就是完全利用器材的自变量。
比如给了7个增砣砝码,但是需要记录6组数据,那么最大上限就是7个增砣对应的质量;那么1-6当中一些数据可以相应地不用做。
Range: \[ L_\text{max} – L_\text{min} >= 30 \text{cm}\]
w14 qp34 Q1(d)
这里的range的也是一分。
3. Column heading:
绘制表格的表头heading,需要写物理量符号,单位unit。如果不写的话,会被扣分;
其次,表头可能还需要相应的计算物理量;比如记录的物理量是T,但是需要研究T2 与其他物理量关系,表头还需要增加这一栏,并且相应地也得附上单位。一个正确的表头如下:
| T/s | L/cm | T2/s2 | 1/L /cm-1 |
Column headings:
Each column heading must contain a quantity and a unit where appropriate.
The presentation of quantity and unit must conform to accepted scientific convention
s18 qp32 Q1(b)
表头的绘制当中,符号,单位都需要标注!
4. Data trend
可能为了方便,我们在改变自变量的时候未必按照趋势。但是在记录数据体现的时候,有额外的一分是将趋势体现出来。建议这里用升序的方式记录数据
Six sets of readings showing the correct trend and without help from the Supervisor scores 4 marks, five sets scores 3 marks etc.
s16 qp34 Q1(d)(ii)
5. precision / smallest division
由于器具的使用,常见仪器不可能得到过高精度,因此需要记录正确的数值
- 塑料尺ruler的记录到0.01cm、或者是0.1mm
- 秒表stopwatch记录到0.01s
- 量角器protractor记录到1°
- 螺旋测微器microscrew guage记录到0.01mm
- 游标卡尺verniercaliper 根据附尺的格子数确定精度,比如10格的精度就是0.1mm,50格的精度是0.02mm
- 电子电流表,电压表,万用表一般是小数点后一位。
Consistency:
All values of t must be given to the nearest 0.1 s, or all to the nearest 0.01 s.
s16 qp34 Q1(d)(ii)
6. indpendent/dependent variablbes
虽然测量的时候会是某两个物理量,但是最终研究线性关系的未必是这两个物理量,可能是两个物理量的变种形式,需要在表头heading的部分体现出来。比如第三点给出例子,要注意两个结果的最小最大值,从而确定grid table当中的scale。
7. Akward scale
P3卷给出的表格如下图所示:

水平方向会有8*10个小格,竖直方向有12*10个小格。
7.1 需要避免awkward scales。比如3个大格:10 unit。这样,每一个最小格的scale就是0.333333333333333333。这不方便去描点。比较好的就是1:10, 2:10, 5:10等。确保每个小格的长度都是可除尽的并且舒服的小数。
7.2 至少使用75%的网格线面积,也就是最小点与最大点的斜对角线连线要超过75%的纸张斜对角线;因此不要选择过小的scale
7.3 坐标轴要从0开始,不能使用折断符号
Sensible scales must be used (no awkward scales, e.g. 3:10 or fractions).
Scales must be chosen so that the plotted points occupy at least half the graph grid in both x and y directions.
w19 qp34 Q1(d)(i)
8. Label in axis
8.1 坐标轴必须进行绘制,并且其中要对坐标轴进行符号/单位的标记,比如T2/s2.
8.2 坐标轴上的数字,间隔不能超过三个大格。
相邻标记不能超过三个大格,
e.g.
1:10的比例关系,在坐标轴上不能标注0, 40, 80。 这样标记相差太远,是4个大格了。
比较合适的标注有 0,10,20,30,40,50,60,70,80;相距1大格
或者是0,20,40,60,80;相距2大格。
Scales must be labelled with the quantity that is being plotted.
Scale markings should be no more than three large squares apart.
w19 qp34 Q1(d)(i)
9. scatterpoints
9.1 散点需要使用 × 进行表示,并且尺寸大小不能超过小格的一半,也就是说,×最大只能占据一个小格的大小。(用圆圈点是可以的,但是三金的学生决不允许,because I am a dictator!)
9.2 ×的中心点,需要在格点上,或者在线上。如果记录数据值没有办法完美落在线或者格点上,允许进行一定程度的近似,近似不超过半个小格的精度即可。
e.g. 横竖方向上一小格都是0.5
(2.0, 2.5)这组数据,两个都能完美地被网格线卡主,所以无需处理,直接描点
(1.5, 2.2)这组数据;由于1.5能卡在格子上,因此2.2可以不用做近似,直接描点。
(0.2,1.2)这组数据;处理方式有两种;一个是处理为(0,1.2)或者是处理为(0.2, 1.0);建议按照第二种方式进行调整。
这些处理的方式都是为了满足×的中心点不能处于格子当中。
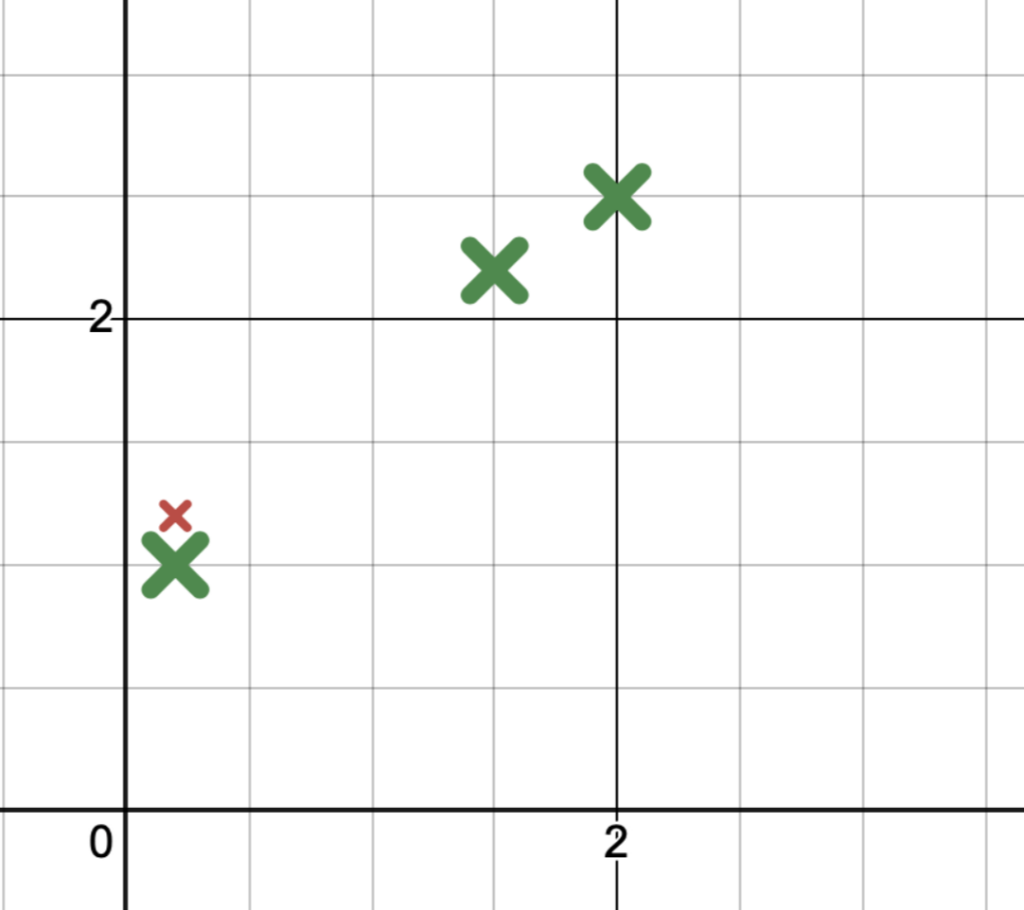
All observations must be plotted.
Diameter of plotted points must be < half a small square (no “blobs”).
Plotted points must be accurate to within half a small square.
All points must be labelled on the grid
s15 qp35 Q(1)(d)i
10. Line of best fit
10.1 拟合线是通过Least Square Method进行求算的,在物理教学当中并不专门解释方法原理,只需要知道通过计算器算出regression line就可以了。casio的拟合分析结果如下图所示
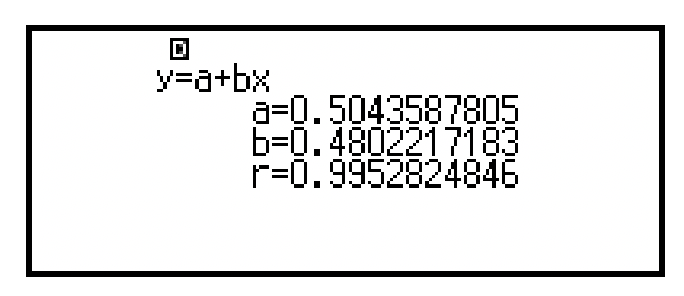
10.2 考官会通过balance of all points来判断,说人话,就是看学生绘制的拟合线的上下侧的散点数量以及residual是否合理,不过也不会这么严格,至少有5个点满足即可。
10.3 如果有一个点偏离拟合线太远,也没有关系,但是需要单独圈出来,标记成为outlier。这个outlier在求算拟合线的时候需要删除掉(重新输入计算器,重新算)。
10.4 为了达到10.1 所说的平衡,建议偷偷地绘制出自变量和因变量的均值点。
\[\bar{x}=\frac{\sum_{i=1}^6 x_i}{6}, \bar{y}=\frac{\sum_{i=1}^6 y_i}{6}\]
然后用透明30cm长尺,穿过该均值点,进行旋转,尽可能让更多的散点里尺更加接近。这里很明显,当尺旋转到紫色线条所处位置时,是散点和拟合线最接近的时候。
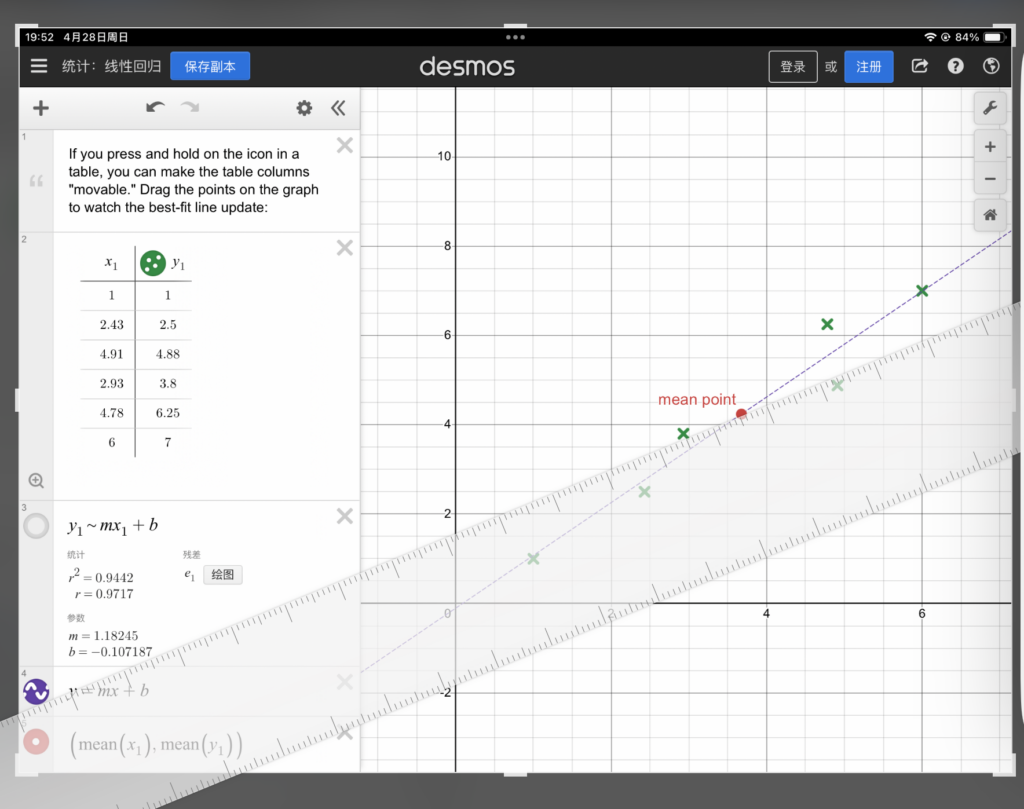
10.5 直线不要画太粗,直线必须直,建议用铅笔绘制,如果满意再用水笔描一遍。
Judge by balance of all points on the grid about the candidate’s line (at least 5 points). There must be an even distribution of points either side of the line along the full length.
Allow one anomalous point only if clearly indicated (i.e. circled or labelled) by the candidate. There must be at least five points left after the anomalous point is disregarded.
Line must NOT be kinked or thicker than half a small square.
11. Gradient
绘制拟合线最重要的目的就是,求算斜率gradient 和截距y-intercept。但实际上这一步在计算器的求算过程中就已经可以求出来了。如casio计算器界面所示。
但是,由于在这次的实验处理当中是大致绘制拟合线,从而根据拟合线算,并没有采用最小二乘回归法。所以需要用非常简单原始的rise/run
\[m = \frac{\Delta y}{\Delta x}\]
11.1 此时需要抛弃掉6组数据,从拟合线上选择在网格线格点上的数据点,标记起来并且记录数据
11.2 绘制\Delta y 和\Delta x的三角形;斜边为拟合线;该三角形斜边需要占据拟合线50%以上的长度
11.3 利用公式求算斜率;并且与计算器中求算的结果进行对比,如果相差不大。则证明求算正确;无需得到与计算器拟合分析完全一致的结果;因为使用这种方法就是仅仅是一种近似估算!
11.4 根据y和x的单位,来确定斜率m的单位!
Gradient sign on answer line matches graph drawn.
The hypotenuse of the triangle used must be greater than half the length of the drawn line. Method of calculation must be correct. Do not allow ∆x / ∆y.
Both read-offs must be accurate to half a small square in both the x and y directions.
s17 qp31 Q1(e)iii
12. y-intercept
同样地,截距y-intercept其实在计算器拟合的过程中也已经自动出来了,但是这里依旧采用考生绘制的拟合线进行预估求算。需要完整地体现过程,CAIE允许两种计算方式:
12.1 根据拟合线和y轴的交点直接读出y-intercept;所以该方法快捷,但是不准确;并且需要在散点图上点出交点
12.2 利用拟合线上的点(x0,y0),以及上一问求算的斜率,计算出y-intercept。公式为:
\[b= y_0 – m\cdot x_0\]
两种方法求算结果应一致,并且应该和计算器求算结果接近。
12.3 y-intercept的单位与y的单位完全一致。
Correct read-off from a point on the line substituted correctly into y = mx + c or an equivalent expression. Read-off accurate to half a small square in both x and y directions.
or
Intercept read directly from the graph, with read-off at x = 0, accurate to half a small square in y direction.
s17 qp31 Q1(e)iii
13. Remaining Parameter
基本上根据给定的公式,确定P,Q与斜率和截距的关系,并且明确单位即可。注意不允许用分数表示
Value of P = candidate’s gradient.
Value of Q = candidate’s intercept.
Correct units for P and Q
w13 qp33 Q1(e)
Question 2
第二条题目是仅需要测量两组数据的实验题,也是20分。但是最大的区别在于这一条题目的实验设计是有很大缺陷的,通常测出来的数据误差都挺大的。不要在意实验数据,因为这里的20分当中有8分是需要寻求出4个缺陷source of error以及对应的四个改进方法。是希望借此考察学生发现实验中的不足和改进的能力。以下是实验二需要注意的地方以及一些常见的套路化回答
1. repeated reading
第一个数据的测量和记录会给两分,这两分当中必定有一分来自于repeated reading。可以通过下标的方式记录多次实验的数据,也可以绘制表格。测量至少两次数据,但是建议测量三次数据。
可以用表格的形式展示多次数据,如下所示
| trial | 1 | 2 | 3 |
| Time/s | 1.12s | 1.15s | 1.35s |
在最后体现出取平均值的过程,并且该数据值也是应该放在答案线上的数据值。
\[
\bar{T} = \frac{T_1+T_2+T_3}{3} = \frac{1.12+1.15+1.35}{3}=1.21s
\]
Value of T with unit.
Evidence of repeats.
s13 qp31 Q2(c)ii
2. percentage uncertainty
必定有一分是求算测量数据值的uncertainty。如果采取了多次测量取均值的方法,那么可以利用
\[
\text{absolute uncertainty} = \frac{\text{max}-\text{min}}{2}
\]
先进行absolute uncertainty的求算,再利用
\[
\text{percentage uncertainty} = \frac{\text{absolute uncertainty}}{\text{average reading}}
\]
求算出percentage uncertainty,最终百分比不确定度保留1个或者2个有效数位即可。
e.g.
\[
\frac{1.35-1.15}{2}/1.21=8\%
\]
Absolute uncertainty in x in range 2 mm–5 mm.
If repeated readings have been taken, then the uncertainty can be half the range (not zero) only if working shown.
Correct method of calculation to obtain percentage uncertainty.
s14 qp31 Q2(b)ii
注意:还有一种方案,是直接用仪器的精度precision,并且进行人为的放大2-5倍。这个人为放大的目的是为了体现还有其他的因素带来误差。建议只测量了一次的同学,或者三次读数的都一样的同学至少把仪器的精度放大3-5倍作为绝对不确定度。进行求算。
3. significant figures
必定有两分考察保留合适的有效数位,以及为什么选择保留这么多有效数位的原因。
要根据之前测量的数据值的有效数位,保留相同的位数,或者多一位。
Justification for significant figures in R linked to significant figures in p and l
w22 qp33 Q2(b)
常见的描述为:
The R should show the same number of significant figures (or one more than the) quantity (or quantities) it is calculated from.
Because p and l has 3 significant figures, the R should have 3 sig fig as well.
4. support relationship
必定有考察两个测量的计算值是否支持某种关系。其实就是根据测量出的两组数据值,利用同样的公式计算出一个参数。当然,如果某种关系显然存在的话,这个参数数值应该是完全一样的。但是无论一样不一样,都可以得到此题的分数。
因为需要做的事情是scientific reasoning。实事求是!核心的做法是:
- 陈述能够接受/拒绝两个数据值是否一致的标准
- 按照标准进行求算
- 比较是否满足标准
- 推出结论
two values of k calculated correctly.
Sensible comment relating to the calculated values of k, testing against a criterion specified by the candidate.
s16 qp33 Q2(f)
这里的criterion有两种标准。
- 两个k值之间的percentage difference小于规定值。一般可以取5% ,10%最多到20%,根据你对这个实验的误差程度的判断。建议一律取5%
- 两个k值之间的percentage difference小于计算值的percentage uncertainty。那么可以接受两个数值比较接近。
所以典型的描述如下:
The percentage difference between the two calculated k values is ……… , it is less/greater than 5%(10%, 20%). So the suggested relationship is supported/not supported.
5. limitations and improvements
这里的8分能拿到6分已经算不错了,7分是神人,8分拿满证明你有点天赋在身!
这个实验就是故意设计地比第一个实验更加的不精确。目的就是考察学生对于实验设计当中不合理之处的感知。所以limitation的四分能拿到的话,相应的改进分也可以拿到。虽然是对能力的考察,但是也是有套路的。其中有两分是套话。不能不会。
5.1 Two sets of data (readings) are not enough to draw a valid conclusion. Hence, take more readings and plot a graph or take more readings and compare k values.
这个问题和改进是所有题目都可以答的,背!
5.2 记录数据太小,以致于容易产生较大的percentage error。比如运动记录的时间很短,大概在1.0s左右。这样的太短太小的时间测量不准确。
5.3 仪器的精度不足,具体的体现是:
5.3.1 利用ruler测量直径,不如利用vernier caliper
5.3.2 利用stopwatch测量时间,不如利用light gate
5.3.3 利用protractor测量小角度(低于10°),不如利用ruler测量邻对斜的直角三角形关系,利用三角比trignometric ratio求算夹角
5.4 实验设计测量数据值,不太容易测量。比如测量悬吊角
5.5 待测物体本身不满足要求。比如要求球形物体,结果是近似球体而不是标准球体
Over